Կլաստերային վերլուծությունը հաճախ անվանում են տիպաբանական վերլուծություն, ավտոմատ դասակարգում:  Այնուամենայիվ սոցիոլոգների, վիճակագիրների և տնտեսագետների մոտ ընդունված է կլաստերային վերլուծություն եզրույթը: 

Կլաստերային վերլուծությունը  իրենից ներկայացնում է միևնույն խմբի հետազոտական օբյեկտների միավորումը կամ միևնույն հատկանիշ ունեցող միավորների խմբավորումը իհակադրություն այդ հատկանիշը չունեցող այլ միավորների:   

Կլաստերային վերլուծությունը օգտագործվում է ժամանակակից  տվյալների վերլուծության հիման վրա ստեղծված համարյա բոլոր ոլորտներում՝ արհեստական ինտելեկտի և մեքենաների ինքնուրույն ուսուցման, պատկերների ավտոմատացված վերլուծության, բիոինֆորմատիկայի և այլն ոլորտներում: 

Կլաստերային վերլուծությունը մեծ հաշվով առանձին մեթոդ չէ, այլ խնդիր է, որը լուծվում է տարբեր մեթոդների և վերլուծական գործիքների կիրառությամբ:  Հաճախ միևնույն հանրույթի տարբեր մեթոդներով կլաստերային վերլուծությունը կարող է հանդիսացնել միմիյանցից զագալիորեն տարբեր կլաստերների առաջացմանը: 

Որպես կանոն կլաստերները առանձնացվում են ընտրելով իրարից առավել մոտ, սահմանափակ ինտերվալ ունեցող խմբերը, կլաստերների միջև հեռավորությունը չափվում է տարբեր բաշխումների, միջին ցուցանիշների և այլ վիճակագրական գործիքների միջոցով: 

Կլաստերների առանձնացումը ավտոմատ չի իրականացվում, այլ հիմնվում է այս կամ այն տեսության կամ ենթադրության վրա: Հաճախ իդեալական կլաստերներ ստանալու փորձերը հանգեցնում են լատենտ և առաջին հայացքից չերևացող մինի կլաստերների անտեսմանը, որի արդյունքում հետազոտության արդյունքները դառնում են խեղաթյուրված:   

Գոյություն ունի վիճակագրական հետազոտության խմբավորման  և կլաստերային վերլուծության միջև  կան սկզբունքային տարբերություններ` չնայած նույնիսկ փորձառու հետազոտողները հաճախ շփոթում են դրանք: 
Վիճակագրական խմբավորումը հիմնված է նախորոք տրված փոփոխականների բաշխումների վրա, իսկ կլաստերային վերլուծությունը հիմնված է այս կամ այն փոփոխականի բնութագրիչների վիճակագրական կուտակումների վրա:  Հետազոտողների կողմից առաջադրված փոփոխականների տիպաբանությունը և բաշխումները, կարող են համընկնել կլաստերների հետ:  Այնուամենայնիվ,  միշտ չէ, որ տեսական տիպաբանության մասին պատկերացումները  համընկնում են իրական վիճակագրական խմբավորումների հետ:  Մյուս ծայրահեղությունն էլ այն է, որ հետազոտողները պատահական համընկնումները դիտարկում են որպես օրինաչափություն: 

Արդյունքների մեկնաբանությունը կլաստերային վերլուծության առավել խոցելի կողմերից է, քանի որ առանց ավելի խորը և բազմակողմանի վերլուծության դժվար է հասկանալ ստացված կլաստերների խմբավորումների իրական պատճառները:  

 Typical cluster models include:

• Connectivity models: Կլաստերները ձևավորվում են իրենց կապերի հիման վրա, որինակ հիերարխիկ մոդելների դեպքում, երբ ավելի բարձր շերտը կապված է ավելի ցածր շերտերի հետ: 
• Centroid models: Ամեն կլաստեր հաշվարկվում է միջին ցուցանիշներով և տրանց շուրջ կուտակումների շնորհիվ: 
• Distribution models: Այս մեդելի դեպքում հաշվի են առնվում փոփոխականների վիճակագրական բաշխումները: 
• Density models: Աշխարհագական տեղաբաշխման կապը այս կամ այն փոփոխականի վիճակագրական բնութագրիչների հետ: 
• Subspace models: կրկնակի կլասերիզացիայի մոդել է, երբ խմբավորվում են ինչպես հետազոտվող միավորները, այնպես էլ 
• Group models: Որոշ մոդելների դեպքում չկան հստակ և կոնկրետ պարամետրներ, որոնց միջոցով հնարավոր է առանձնացնել կլաստերները՝ փոխարենը կան խմբային բնութագրիչներ (a, b c ...n)
• Graph-based models: 

A "clustering" is essentially a set of such clusters, usually containing all objects in the data set. Additionally, it may specify the relationship of the clusters to each other, for example a hierarchy of clusters embedded in each other. Clusterings can be roughly distinguished as:

• hard clustering: each object belongs to a cluster or not
• soft clustering (also: fuzzy clustering): each object belongs to each cluster to a certain degree (e.g. a likelihood of belonging to the cluster)

There are also finer distinctions possible, for example:

• strict partitioning clustering: here each object belongs to exactly one cluster
• strict partitioning clustering with outliers: objects can also belong to no cluster, and are considered outliers.
• overlapping clustering (also: alternative clustering, multi-view clustering): while usually a hard clustering, objects may belong to more than one cluster.
• hierarchical clustering: objects that belong to a child cluster also belong to the parent cluster
• subspace clustering: while an overlapping clustering, within a uniquely defined subspace, clusters are not expected to overlap.
• Linkage clustering examples
• 

  Single-linkage on Gaussian data. At 35 clusters, the biggest cluster starts fragmenting into smaller parts, while before it was still connected to the second largest due to the single-link effect.

• 

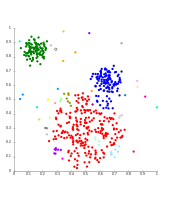
  Single-linkage on density-based clusters. 20 clusters extracted, most of which contain single elements, since linkage clustering does not have a notion of "noise".

• k-Means clustering examples
• 

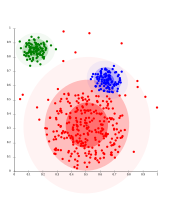
  K-means separates data into Voronoi-cells, which assumes equal-sized clusters (not adequate here)

• 

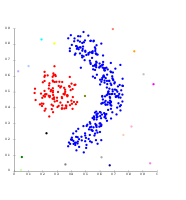
  K-means cannot represent density-based clusters

• Expectation-Maximization (EM) clustering examples
• 

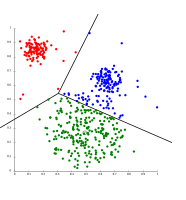
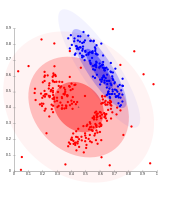
  On Gaussian-distributed data, EM works well, since it uses Gaussians for modelling clusters

• 

  Density-based clusters cannot be modeled using Gaussian distributions

   

  .

• Density-based clustering examples
• 

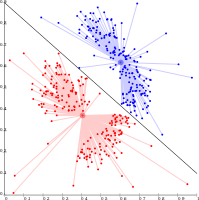
  Density-based clustering with DBSCAN.

• 

  DBSCAN assumes clusters of similar density, and may have problems separating nearby clusters

• 

  OPTICS is a DBSCAN variant that handles different densities much better

Market research

Cluster analysis is widely used in market research when working with multivariate data from surveys and test panels. Market researchers use cluster analysis to partition the general population of consumers into market segments and to better understand the relationships between different groups of consumers/potential customers, and for use in market segmentation, Product positioning, New product development and Selecting test markets.

Grouping of shopping items

Clustering can be used to group all the shopping items available on the web into a set of unique products. For example, all the items on eBay can be grouped into unique products. (eBay doesn't have the concept of a SKU)Social science

Crime analysis

Cluster analysis can be used to identify areas where there are greater incidences of particular types of crime. By identifying these distinct areas or "hot spots" where a similar crime has happened over a period of time, it is possible to manage law enforcement resources more effectively.

Educational data mining

Cluster analysis is for example used to identify groups of schools or students with similar properties.

Typologies

From poll data, projects such as those undertaken by the Pew Research Center use cluster analysis to discern typologies of opinions, habits, and demographics that may be useful in politics and marketing.

Others

Field robotics

Clustering algorithms are used for robotic situational awareness to track objects and detect outliers in sensor data.

Mathematical chemistry

To find structural similarity, etc., for example, 3000 chemical compounds were clustered in the space of 90 topological indices.

Climatology

To find weather regimes or preferred sea level pressure atmospheric patterns.

Petroleum geology

Cluster analysis is used to reconstruct missing bottom hole core data or missing log curves in order to evaluate reservoir properties.

Physical geography

The clustering of chemical properties in different sample locations.