| Home » Articles » Հոդվածներ |
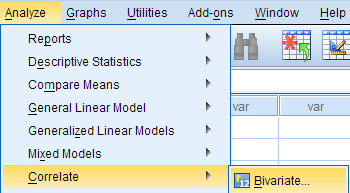
To run a bivariate Pearson Correlation in SPSS, click Analyze > Correlate > Bivariate.
The Bivariate Correlations window opens, where you will specify the variables to be used in the analysis. All of the variables in your dataset appear in the list on the left side. To select variables for the analysis, select the variables in the list on the left and click the blue arrow button to move them to the right, in the Variables field.
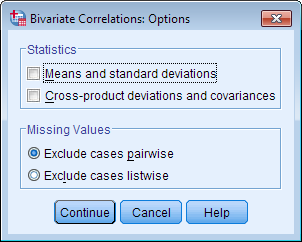
AVariables: The variables to be used in the bivariate Pearson Correlation. You must select at least two continuous variables, but may select more than two. The test will produce correlation coefficients for each pair of variables in this list. BCorrelation Coefficients: There are multiple types of correlation coefficients. By default, Pearson is selected. Selecting Pearson will produce the test statistics for a bivariate Pearson Correlation. CTest of Significance: Click Two-tailed or One-tailed, depending on your desired significance test. SPSS uses a two-tailed test by default. DFlag significant correlations: Checking this option will include asterisks (**) next to statistically significant correlations in the output. By default, SPSS marks statistical significance at the alpha = 0.05 and alpha = 0.01 levels, but not at the alpha = 0.001 level (which is treated as alpha = 0.01) EOptions: Clicking Options will open a window where you can specify which Statistics to include (i.e., Means and standard deviations, Cross-product deviations and covariances) and how to address Missing Values (i.e., Exclude cases pairwise or Exclude cases listwise). Note that the pairwise/listwise setting does not affect your computations if you are only entering two variable, but can make a very large difference if you are entering three or more variables into the correlation procedure.
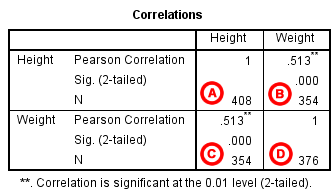
TABLESThe results will display the correlations in a table, labeled Correlations.
A Correlation of Height with itself (r=1), and the number of nonmissing observations for height (n=408). B Correlation of height and weight (r=0.513), based on n=354 observations with pairwise nonmissing values. C Correlation of height and weight (r=0.513), based on n=354 observations with pairwise nonmissing values. D Correlation of weight with itself (r=1), and the number of nonmissing observations for weight (n=376). The important cells we want to look at are either B or C. (Cells B and C are identical, because they include information about the same pair of variables.) Cells B and C contain the correlation coefficient for the correlation between height and weight, its p-value, and the number of complete pairwise observations that the calculation was based on. The correlations in the main diagonal (cells A and D) are all equal to 1. This is because a variable is always perfectly correlated with itself. Notice, however, that the sample sizes are different in cell A (n=408) versus cell D (n=376). This is because of missing data -- there are more missing observations for variable Weight than there are for variable Height. If you have opted to flag significant correlations, SPSS will mark a 0.05 significance level with one asterisk (*) and a 0.01 significance level with two asterisks (0.01). In cell B (repeated in cell C), we can see that the Pearson correlation coefficient for height and weight is .513, which is significant (p < .001 for a two-tailed test), based on 354 complete observations (i.e., cases with nonmissing values for both height and weight). | |
| Views: 879 | |
| Total comments: 0 | |